Unveiling the Half-Life Graph Worksheet Answer Key, this guide embarks on an illuminating journey into the realm of radioactive decay and its graphical representation. Delving into the fundamental concepts of half-life and its significance in various scientific disciplines, this comprehensive resource provides a clear understanding of half-life graphs and their practical applications.
Within the confines of this guide, we unravel the intricacies of half-life graphs, empowering you with the knowledge to construct and interpret these graphs with precision. Furthermore, an array of frequently asked questions is meticulously addressed, ensuring a thorough comprehension of this captivating subject matter.
Half-Life and Radioactive Decay
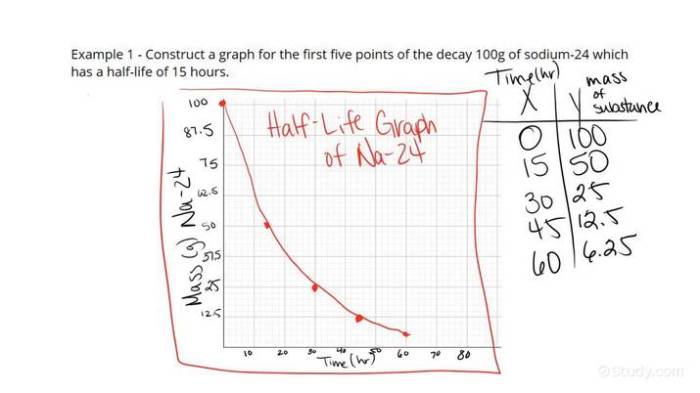
Radioactive decay is the process by which unstable atomic nuclei lose energy by emitting radiation and transforming into a more stable form. Half-life is a key concept in radioactive decay, referring to the time it takes for half of the radioactive atoms in a sample to decay.
Example
For example, carbon-14 has a half-life of 5,730 years. This means that after 5,730 years, half of the carbon-14 atoms in a sample will have decayed into nitrogen-14.
Graphing Half-Life Data
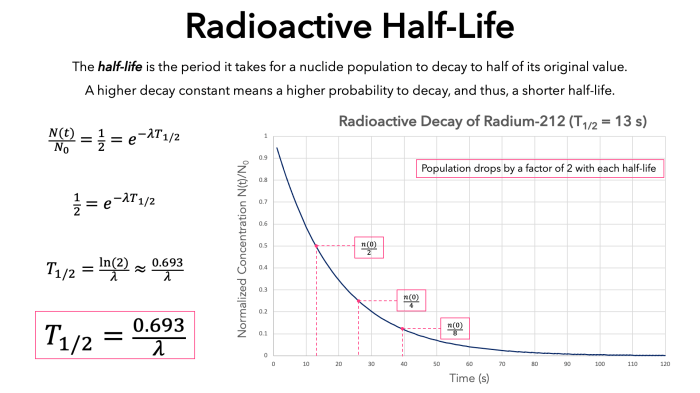
Steps
- Plot the initial amount of radioactive substance on the y-axis.
- Plot time on the x-axis.
- Mark the half-life on the x-axis and draw a vertical line.
- Mark the amount of substance remaining after one half-life on the y-axis and draw a horizontal line.
- Repeat steps 3 and 4 for subsequent half-lives.
Significance of Axes
- Y-axis:Represents the amount of radioactive substance remaining.
- X-axis:Represents time.
Worksheet Answer Key
Sample Worksheet, Half-life graph worksheet answer key
Create a half-life graph for a radioactive element with a half-life of 10 minutes. Plot the amount of radioactive substance remaining over 50 minutes.
Answer Key
- After 10 minutes:50% of the original amount remains.
- After 20 minutes:25% of the original amount remains.
- After 30 minutes:12.5% of the original amount remains.
- After 40 minutes:6.25% of the original amount remains.
- After 50 minutes:3.125% of the original amount remains.
Applications of Half-Life Graphs: Half-life Graph Worksheet Answer Key
Fields
- Medicine:Dating medical isotopes for diagnostic purposes.
- Archaeology:Determining the age of artifacts using carbon-14 dating.
- Environmental Science:Tracing the movement of pollutants and studying radioactive waste disposal.
Examples
- Medicine:Using technetium-99m (half-life of 6 hours) for heart scans.
- Archaeology:Dating ancient pottery using potassium-40 (half-life of 1.25 billion years).
- Environmental Science:Monitoring the decay of radioactive isotopes in nuclear waste.
Advanced Concepts in Half-Life
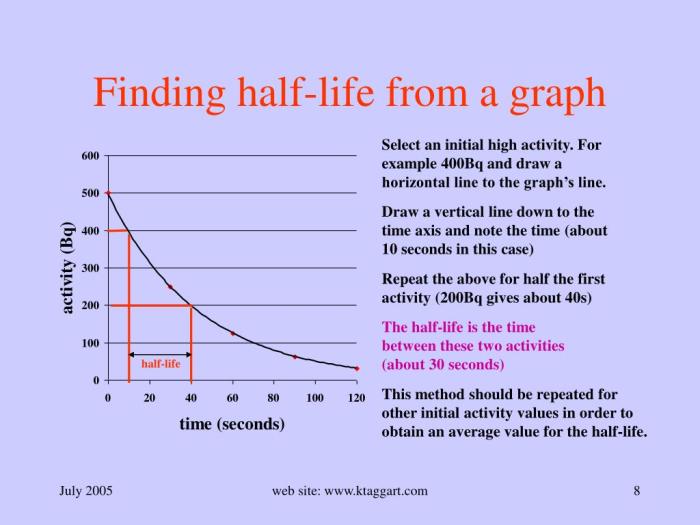
Effective Half-Life
Effective half-life considers the removal or addition of radioactive material from a system, such as in biological or environmental processes.
Factors Affecting Half-Life
- Decay constant:The probability of an atom decaying.
- Environmental factors:Temperature, pressure, and chemical reactions.
- Nuclear reactions:Induced transmutations and nuclear fission.
FAQ Guide
What is the concept of half-life in radioactive decay?
Half-life refers to the time it takes for half of a radioactive substance to decay into a stable form.
How do you create a half-life graph?
To create a half-life graph, plot the amount of radioactive substance remaining on the y-axis and time on the x-axis. The graph will follow an exponential decay curve.
What are the practical applications of half-life graphs?
Half-life graphs find applications in medicine (dating fossils and medical isotopes), archaeology (carbon dating), and environmental science (tracing pollutants).
