Home Mathematics Use The Similarity Relationship To Find The Indicated Value

Use The Similarity Relationship To Find The Indicated Value

May 15, 2024

Use the similarity relationship to find the indicated value – Delving into the realm of similarity relationships, we embark on a captivating journey to uncover the hidden power behind finding indicated values. These relationships serve as a beacon of clarity, guiding us towards precise determinations within complex scenarios. As we delve deeper, we shall unravel the intricate methods, explore diverse applications, and conquer the limitations associated with this invaluable tool.

Similarity Relationship: Use The Similarity Relationship To Find The Indicated Value

Use the similarity relationship to find the indicated value

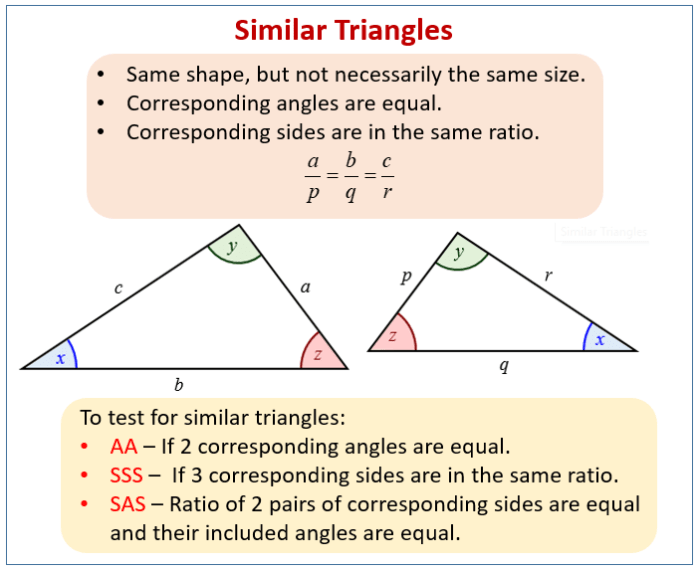
The similarity relationship is a mathematical concept that describes the similarity between two geometric figures. It is used to find the indicated value of a figure when given the measurements of a similar figure.

Methods for Using Similarity Relationship

  1. Determine if the two figures are similar. Similar figures have the same shape but not necessarily the same size.
  2. Identify the corresponding sides or angles of the two figures.
  3. Set up a proportion using the corresponding sides or angles.
  4. Cross-multiply the proportion to solve for the unknown value.

Example:

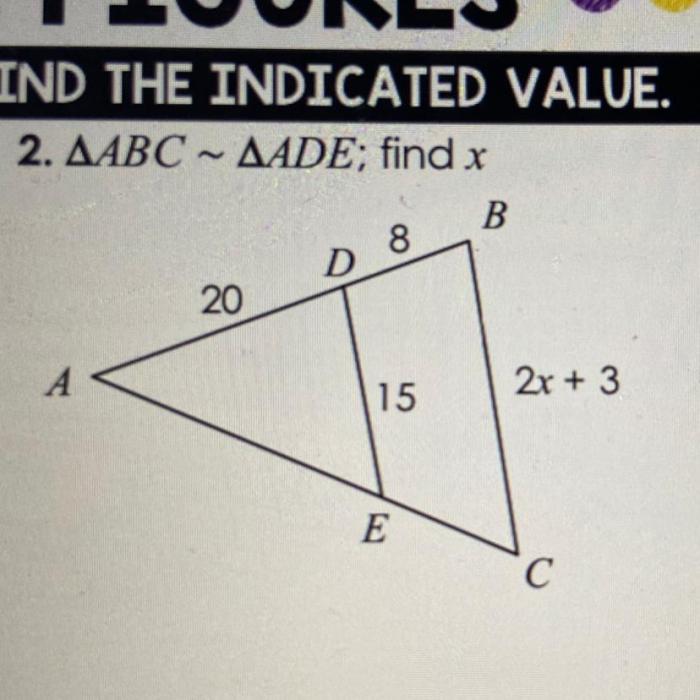
Find the length of the missing side of the triangle below if the triangle is similar to the one shown.

Triangle with missing side

Solution:

  1. Set up a proportion using the corresponding sides:

    2. $$\frac68 = \fracx10$$

  2. Cross-multiply to solve for x:

    3. $$6 \times 10 = 8x$$ $$x = 7.5$$

  3. Therefore, the length of the missing side is 7.5.

Examples of Similarity Relationship Applications, Use the similarity relationship to find the indicated value

Common Queries

What is the fundamental concept behind similarity relationships?

Similarity relationships establish a proportional connection between two or more geometric figures or algebraic expressions, allowing us to deduce unknown values based on known similarities.

How do I determine the indicated value using a similarity relationship?

To find the indicated value, identify the known and unknown values within the similarity relationship. Then, set up a proportion and solve for the unknown value.

What are the limitations of using similarity relationships?

Similarity relationships are limited to scenarios where the figures or expressions exhibit proportional relationships. Additionally, they may not be applicable in cases involving non-similar figures or expressions.

Use the similarity relationship to find the indicated value
Indicated urgent similarity relationship

You May Also Like

Unit 3 parent functions and transformations homework 2

Unit 3 Parent Functions And Transformations Homework 2

Big ideas math geometry 9.2 answers

Big Ideas Math Geometry 9.2 Answers

Application Procedure Example
Finding the height of a tree Measure the height of a similar object (e.g., a flagpole) and the length of its shadow. Then measure the length of the tree’s shadow and use the similarity relationship to find the height of the tree. A flagpole that is 10 feet tall casts a shadow that is 6 feet long. A nearby tree casts a shadow that is 12 feet long. Find the height of the tree.
Enlarging or reducing a map Use the similarity relationship to find the scale factor between the original map and the enlarged or reduced map. Then use the scale factor to determine the new measurements on the map. A map of a city is drawn on a scale of 1 inch to 1 mile. To create a larger map, the scale factor is increased to 2 inches to 1 mile. Find the new length of a road that is 5 miles long on the original map.