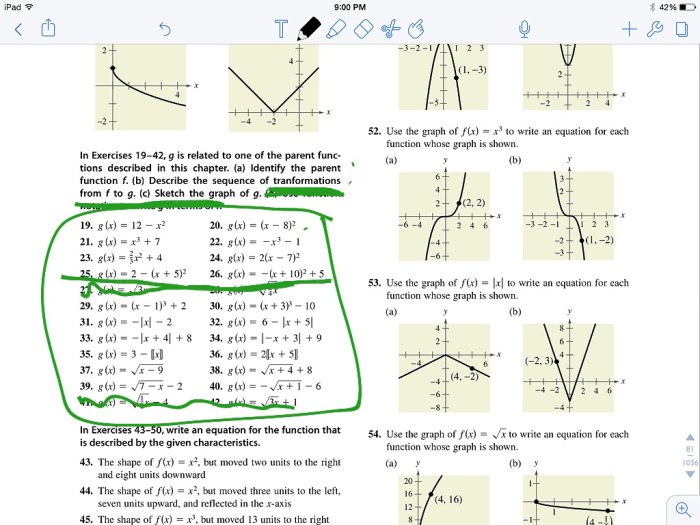
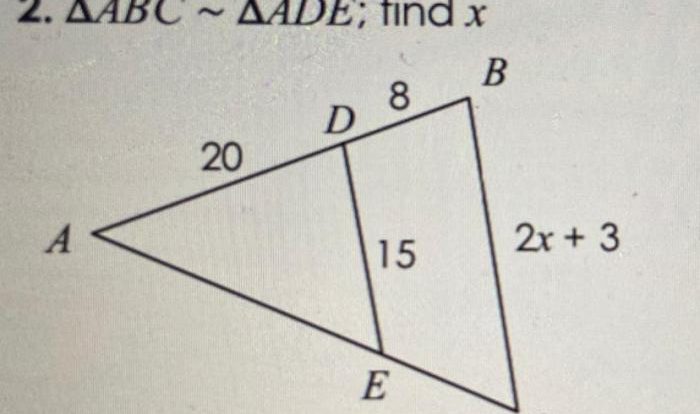
Embark on a mathematical odyssey with Unit 3 Parent Functions and Transformations Homework 2, where you’ll unravel the secrets of manipulating graphs and transforming functions. This assignment delves into the fundamental concepts of parent functions and the diverse array of transformations that can reshape their graphs, empowering you to analyze and interpret complex functions with precision.
Prepare to explore the properties and characteristics of common parent functions, including linear, quadratic, exponential, and logarithmic functions. Discover the power of transformations, such as translations, reflections, rotations, and dilations, and witness their profound impact on the shape and position of graphs.
Through engaging examples and visual representations, you’ll gain a comprehensive understanding of how transformations alter the behavior of functions, equipping you with the tools to solve real-world problems and deepen your mathematical knowledge.
Unit 3: Parent Functions and Transformations: Unit 3 Parent Functions And Transformations Homework 2

Dalam matematika, fungsi induk atau parent function adalah fungsi dasar yang mewakili bentuk umum dari sekelompok fungsi terkait. Fungsi-fungsi ini memiliki sifat dan karakteristik yang serupa, yang membuatnya menjadi titik awal yang berguna untuk mempelajari dan memahami berbagai jenis fungsi.
Parent Functions
Fungsi induk yang umum meliputi:
- Fungsi Linear:f(x) = mx + b
- Fungsi Kuadrat:f(x) = ax² + bx + c
- Fungsi Eksponensial:f(x) = a^x
- Fungsi Logaritmik:f(x) = log ax
Transformations
Transformasi adalah operasi yang diterapkan pada fungsi untuk menghasilkan fungsi baru. Transformasi dapat digunakan untuk mengubah posisi, bentuk, atau orientasi grafik fungsi.
Jenis transformasi yang umum meliputi:
- Translasi:Memindahkan grafik fungsi ke atas, ke bawah, ke kiri, atau ke kanan.
- Refleksi:Membalik grafik fungsi terhadap sumbu x atau y.
- Rotasi:Memutar grafik fungsi di sekitar titik tertentu.
- Dilatasi:Memperbesar atau memperkecil grafik fungsi.
Homework Assignment 2, Unit 3 parent functions and transformations homework 2
Untuk pekerjaan rumah ini, Anda diminta untuk:
- Menjelaskan konsep fungsi induk dan transformasi.
- Mengidentifikasi jenis-jenis fungsi induk dan transformasi.
- Menerapkan transformasi pada fungsi induk untuk membuat fungsi baru.
- Membuat ilustrasi untuk menunjukkan efek transformasi pada grafik fungsi.
Application and Examples
| Parent Function | Transformation | Example | Effects |
|---|---|---|---|
| Linear | Translasi | f(x) = 2x + 3 | Bergeser 3 unit ke atas |
| Kuadrat | Refleksi terhadap sumbu x | f(x) =
|
Membuka ke bawah |
| Eksponensial | Rotasi 90 derajat berlawanan arah jarum jam | f(x) = 2-x | Grafik menjadi fungsi logaritmik |
| Logaritmik | Dilatasi | f(x) = log2(3x) | Grafik diperluas secara horizontal dengan faktor 3 |
Visual Representations
Berikut adalah beberapa ilustrasi yang menunjukkan efek transformasi pada grafik fungsi:
Gambar 1:Grafik fungsi linear f(x) = x (garis lurus) sebelum dan sesudah translasi 2 unit ke atas (garis putus-putus).
Gambar 2:Grafik fungsi kuadrat f(x) = x² (parabola) sebelum dan sesudah refleksi terhadap sumbu x (parabola terbalik).
Gambar 3:Grafik fungsi eksponensial f(x) = 2 x(kurva naik) sebelum dan sesudah rotasi 90 derajat berlawanan arah jarum jam (kurva menurun).
Gambar 4:Grafik fungsi logaritmik f(x) = log 2x (kurva turun) sebelum dan sesudah dilatasi dengan faktor 3 (kurva lebih lebar).
FAQs
What are the key concepts covered in this homework assignment?
This assignment focuses on parent functions and transformations, exploring their properties, characteristics, and the impact of transformations on their graphs.
How can I approach this assignment effectively?
Begin by understanding the concepts of parent functions and transformations. Then, practice applying transformations to different parent functions and analyze the resulting graphs. Utilize the examples and visual representations provided in the assignment for guidance.
What are the benefits of mastering transformations?
Transformations empower you to manipulate and analyze functions, solve real-world problems, and gain a deeper understanding of the behavior of functions.